visualization and analysis of positional chess graphs
SoftwareX, 2019, in press
Abstract
The game of chess is undoubtedly one of the most popular two-player strategy board games in history, enjoyed by casual players and competing celebrated professionals alike, and serves as prototype research subject in a vast variety of fields. Although a plethora of parsers on a large number of different platforms is readily available for processing records of chess games provided in online databases, Mathematica remains, somewhat surprisingly, exempt. ChessY attempts to fill this gap, by providing a simple set of tools for handling Portable Game Notation (PGN) chess records and their translation into positional chess graphs, thus opening the door for a systematic analysis of chess games within the powerful confines of graph theory using Mathematica.
Supplementary Information and Material
The ChessY toolbox (v1.0) for Mathematica (v10.0 or above) can be downloaded here. Files include:
| ChessY.m | ChessY toolbox (v1.0) |
| README.txt | ChessY manual |
| example*.pgn | example PGN records used in the manual |
| pieces/* | directory with vector graphics of chess pieces |
Please note that ChessY is in active development. Feel free to contact me for general feedback and comments, bug fixes, problems as well as feature requests and suggestions.
Manual
- Data Objects, Constants and Auxiliary Functions
- Chess Position Generation
- Chess Graph Generation
- Visualization
- Chess Graph Analysis
- Examples
Data Objects, Constants and Auxiliary Functions
ChessY is build around three principal types of data objects: position, nodes and edges. While the position object contains a list of pieces and their location on the chessboard, thus uniquely encodes a given chess position, nodes and edges are lists which characterize the chess graph associated with a given position.
Position Data Object
The position data object is a Mathematica list containing two elements:
position = { SUPPLEMENTARY_INFO , LIST_OF_OCCUPIED_SQUARES }Here, SUPPLEMENTARY_INFO is a key-value association list containing supplementary information which characterize a given chess position. This association list has the form
SUPPLEMENTARY_INFO = <| "enpassant"->VALUE ,
"castling"->VALUE ,
"check"->VALUE ,
"checkmate"->VALUE |>where:
-
"enpassant"indicates the node ID (see below) of the target node of a possible en passant move
default value:0 -
"castling"contains information about possible castling moves in form of a list
{ { QSwhite , KSwhite } , { QSblack , KSblack } }
with:QSwhite = True/Falsefor white queenside castlingKSwhite = True/Falsefor white kingside castlingQSblack = True/Falsefor black queenside castlingKSblack = True/Falsefor black kingside castling
{{True,True},{True,True}} -
"check"indicates whether a check was issued in the given position usingTrue/False
default value:False -
"checkmate"indicates whether a checkmate was issued in the given position usingTrue/False
default value:False
The LIST_OF_OCCUPIED_SQUARES entry is a list of elements of type
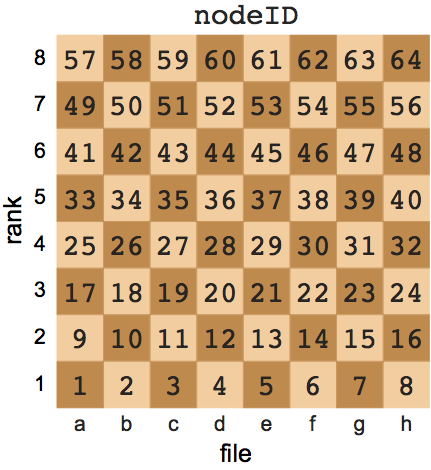
LIST_OF_OCCUPIED_SQUARES = { { nodeID , pieceID } , { nodeID , pieceID } , ... }containing the set of all occupied squares or nodes. Here, nodeID is a unique identifier of each chessboard square, ranging from 1 to 64, starting in the lower left-hand corner with the $a1$ square and ending in the upper right-hand corner ($h8$ square). That is,
|
|
Table 1 file/rank-node ID mapping utilized in ChessY |
For mapping the file/rank chessboard square identifier to the nodeID, see File/Rank-NodeID Mapping.
The pieceID is a unique identifier for the chess piece type:
|
Table 2 Chess piece identification utilized in ChessY |
EXAMPLES:
empty chess board:
positionEmpty =
{
<| "enpassant"->0,
"castling"->{{True,True},{True,True}},
"check"->False,
"checkmate"->False |>,
{}
};initial chess position:
positionStart =
{
<| "enpassant"->0,
"castling"->{{True,True},{True,True}},
"check"->False,
"checkmate"->False |>,
{
{1,wR},{2,wN},{3,wB},{4,wQ},{5,wK},{6,wB},{7,wN},{8,wR},
{9,wP},{10,wP},{11,wP},{12,wP},{13,wP},{14,wP},{15,wP},{16,wP},
{49,bP},{50,bP},{51,bP},{52,bP},{53,bP},{54,bP},{55,bP},{56,bP},
{57,bR},{58,bN},{59,bB},{60,bQ},{61,bK},{62,bB},{63,bN},{64,bR}
}
};position of move 11 in match Spassky-Fischer during the 8th World Championship on Jul 16, 1972:
position23SpasskyFischer1972 =
{
<| "enpassant"->0,
"castling"->{{False,False},{False,False}},
"check"->False,
"checkmate"->False |>,
{
{1,wR},{3,wB},{6,wR},{7,wK},{9,wP},{10,wP},{11,wQ},{12,wN},
{13,wB},{14,wP},{15,wP},{16,wP},{19,wN},{29,wP},{35,bP},{36,wP},
{40,bN},{44,bP},{47,bP},{49,bP},{50,bP},{52,bN},{54,bP},{55,bB},
{56,bP},{57,bR},{59,bB},{60,bQ},{61,bR},{63,bK}
}
};Nodes Data Object
The nodes data object
nodes = { NODE_STATE , NODE_STATE , ... }is a 1-dimensional list (vector) of length 64 with element $i$ containing the node state of node $i$. The NODE_STATE value characterizes each node, and can take various values depending on an optional argument State which can be chosen in many functions of ChessY (see below). Specifically,
-
State->"Piece"the node state indicates the type of piece occupying the node, according to Table 2 -
State->"Color"the node state indicates the color of the piece occupying the node:
color node state white -1 black 1 none 0 Table 3: Node states distinguising
the color of the chess piece -
State->"Simple"the node state indicates whether a node is occupied or not:
square occupied node state yes 1 no 0 Table 4: Node states distinguising
the occupation state of a square
Edges Data Object
The edges data object
edges = { EDGE , EDGE , ... }is a 2-dimensional list (matrix), specifically a variable-length list with elements of the form
EDGE = { SOURCE_NODE_ID , TARGET_NODE_ID , EDGE_STATE }where the edge EDGE_STATE is equal to the color state of the source node (Table 3).
File/Rank-NodeID Mapping
Each square on the chessboard is uniquely labelled in terms of file (a,b,...,h) and rank (1,2,...,8). In order to simplify the mapping between file/rank and node ID (Table 1), ChessY associates each file with numbers: $a \rightarrow 1$, $b \rightarrow 2$, ..., $h \rightarrow 8$. For converting between file, rank and node IDs, ChessY provides three functions:
node ID $\rightarrow$ file:
file[ NODE_ID ]node ID $\rightarrow$ rank:
rank[ NODE_ID ]file/rank $\rightarrow$ node ID:
node[ FILE , RANK ]Moves
In order to generate positional chess graphs from given chess positions, Chessy employs 2-dimensional data arrays which effectively encode all possible moves for each type of chess piece:
-
mN,mNE,mE,mSE,mS,mSW,mW,mNWlists providing the nodes in each of the cardinal and intercardinal directions (N,NE,E,SE,S,SW,W,NW), indexed by the node of origin; these lists are used to generate edges for queen, rook and bishop -
mKingstandard moves of the white/black king -
mKnightstandard moves of the white/black knight -
mwPawn,mbPawnstandard moves of the white/black pawn -
mwPawnR,mbPawnRadditional rank 2/7 move of the white/black pawn -
mwPawnX,mbPawnXcapture moves of the white/black pawn -
mwPawnEP,mbPawnEPen passant moves of the white/black pawn -
enPassantXw,enPassantXben passant target nodes, indexed by the target node of the opposing pawn subject to potential en passant capture; the lists contain the allowed values for the en passant variable used during the evaluation of game positions
Visualization
Additional graphical objects are required to visualize a given chess position in the classical style. These objects are imported as EPS files residing in the subdirectory pieces/.
Chess Position Generation
ChessY provides two ways to generate chess positions, a manual one and by parsing PGN chess records.
Manual Generation
ChessY has two functions for populating a chess board manually with chess pieces, thus creating valid chess positions. Using the function
getPositionFromPieceFileRank[ { p1 , p2 , ... } ]pieces p1, p2, ... can be placed on the board by specifying the piece color and type, as well as the file and rank of the target square. Entries in the argument list must be of the form
p* = COLOR/TYPE/FILE/RANKThe function takes optional arguments:
-
EnPassantFile/Rank of the target node of a possible en passant move
default value:enPassant->0 -
Castlingpossible castling moves in the given position in form of{{QSwhite,KSwhite},{QSblack,KSblack}}(see Position Data Object)
default value:Castling->{{True,True},{True,True}} -
Checkcheck issued in generated position (True/False)
default value:Check->False -
Checkmatecheckmate issued in generated position (True/False)
default value:checkmate->False
EXAMPLES:
identification of white queen on square $a1$:
wQa1chess position with a white queen on $c5$ and a black king on $e8$:
position = getPositionFromPieceFileRank[ {wQc5,bKe8} ];ply 29 in Pietzcker Christmas Tournament (1928) between Gundersen and Faul:
position = getPositionFromPieceFileRank[
{
wRa1,wBc1,wKe1,wRh1,wPa2,wPb2,wPf2,wPg2,wNc3,
wQg4,wPe5,wPh5,wNe6,bRa8,bBc8,bQd8,bRf8,bPa7,
bPb7,bNe7,bKh6,bPd5,bPf5,bPg5,bBb4,bNd4
},
EnPassant->g6,
Castling->{{True,True},{False,False}},
Check->False,
Checkmate->False
];The function
getPositionFromPieceNode[ { p1 , p2 , ... } ]generates a position by populating a chess graph's nodes with pieces p1, p2 identified by
p* = COLOR/TYPE/NODE_IDwhere NODE_ID ranges from 1 to 64 (see Position Data Object). Optional arguments are the same as for getPositionFromPieceFileRank[], except that the value of the EnPassant option is a node ID.
EXAMPLES:
identification of white queen on square $a1$:
wQ1chess position with a white queen on node 35 ($c5$) and a black king on node 61 ($e8$):
position = getPositionFromPieceNode[ {wQ35,bK61} ];ply 29 in Pietzcker Christmas Tournament (1928) between Gundersen and Faul:
position = getPositionFromPieceNode[
{
wR1,wB3,wK5,wR8,wP9,wP10,wP14,wP15,wN19,wQ31,
wP37,wP40,wN45,bR57,bB59,bQ60,bR62,bP49,bP50,
bN53,bK48,bP36,bP38,bP39,bB26,bN28
},
EnPassant->g6,
Castling->{{True,True},{False,False}},
Check->False,
Checkmate->False
];PGN Parser
The second way to generate chess positions is to utilize ChessY's PGN parser, which processes PGN-formatted chess game records. Two functions are available, with the first being (internally) used to get specific information of the move from a single PGN-formatted string, and the second for parsing a whole PGN game record. Only the latter returns a list of chess positions.
The function
parsePGNMove[ MOVE ]parses a single PGN compliant chessmove string and returns a list with details of the move. Please note that this is a very baseline parser for PNG-formatted strings which might not cover deviations from the SAN format recommended by FISA as well as special cases. This function is merely employed for internal purposes, so use with care!
The function returns a list with 11 elements
{
PIECE , FILE , RANK , CAPTURE , DISAMBIGUATION , CASTLING ,
ENPASSANT , PROMOTION , CHECK , CHECKMATE , RESULT
}where:
-
PIECE,FILE,RANKstrings identifying the moved piece as well as strings containing the target file and rank of the moved piece -
CAPTURETrue/Falsedepending on whether the move was a capture move -
DISAMBIGUATIONstring with the departure file or rank provided as disambiguation in the PGN record -
CASTLINGstring with castling information (see Position Data Object) -
ENPASSANTTrue/Falsedepending on whether move was an en passant capture move -
PROMOTIONstring with the identifier of the new promoted piece in the case the move was a promotion -
CHECKTrue/Falseif move leads to check -
CHECKMATETrue/Falseif move leads to checkmate -
RESULTstring containing PGN marker for game result
The function
getPositionsFromGamePGN[ MOVES ]provides the actual PGN game record parser of ChessY. It takes a list of PGN-formatted move strings as argument, and returns a list of all successive positions of the chess game. ChessY provides three example records, each containing the full PGN-compliant record of a single game.
The parser can be used in the following way:
(* load the ChessY toolbox *)
Get["ChessY.m"];
(* open PGN record file *)
pgnfile = OpenRead["example1.pgn"];
eof = False;
(* setup list for handling data *)
game = Array[0,11];
{
cEvent,cSite,cDate,cRound,cWhite,cBlack,cResult,cECO,cWhiteElo,cBlackElo,cMoves
} = Table[i,{i,1,11}];
(* parse PGN record *)
While[ !eof ,
If[
(record = Read[pgnfile,Record,RecordSeparators->{"\n"}])==EndOfFile ,
eof = True
];
If[
(!eof) && (StringTake[record,7]=="[Event ") ,
game[[cEvent]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,6]=="[Site ") ,
game[[cSite]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,6]=="[Date ") ,
game[[cDate]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,7]=="[Round ") ,
game[[cRound]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,7]=="[White ") ,
game[[cWhite]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,7]=="[Black ") ,
game[[cBlack]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,8]=="[Result ") ,
game[[cResult]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,5]=="[ECO ") ,
game[[cECO]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,10]=="[WhiteElo ") ,
game[[cWhiteElo]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,10]=="[BlackElo ") ,
game[[cBlackElo]] = StringSplit[record,"\""][[2]]
];
If[
(!eof) && (StringTake[record,2]=="1.") ,
game[[cMoves]] = StringTrim[
StringSplit[record,RegularExpression["[0-9]+[\\.]"]]
]
];
];
(* close PGN record file *)
Close[pgnfile];
(* get list of game positions from moves *)
positions = getPositionsFromGamePGN[game[[cMoves]]];
(* print result *)
Print[
Panel[
Text[
Grid[
{
{
Style["Event \t",Black,Bold,FontFamily->"Arial",FontSize->12 ],
Style[game[[cEvent]],Black,FontFamily->"Arial",FontSize->12 ]
},
{
Style["Site \t",Black,Bold,FontFamily->"Arial",FontSize->12 ],
Style[game[[cSite]],Black,FontFamily->"Arial",FontSize->12 ]
},
{
Style["Date \t",Black,Bold,FontFamily->"Arial",FontSize->12 ],
Style[game[[cDate]],Black,FontFamily->"Arial",FontSize->12 ]
},
{
Style["Round \t",Black,Bold,FontFamily->"Arial",FontSize->12 ],
Style[game[[cRound]],Black,FontFamily->"Arial",FontSize->12 ]
},
{
Style["White \t",Black,Bold,FontFamily->"Arial",FontSize->12 ],
Style[game[[cWhite]],Black,FontFamily->"Arial",FontSize->12 ]
},
{
Style["Black \t",Black,Bold,FontFamily->"Arial",FontSize->12 ],
Style[game[[cBlack]],Black,FontFamily->"Arial",FontSize->12 ]
},
{
Style["Result \t",Black,Bold,FontFamily->"Arial",FontSize->12 ],
Style[game[[cResult]],Black,FontFamily->"Arial",FontSize->12 ]
}
}
]
] , FrameMargins->{{30, 30}, {10, 10}}
]
];
Print[game[[cMoves]]];
Print[positions];The output will be a formatted box with information about the game, a list of moves, and a list of positions:

Chess Graph Generation
A positional chess graph is fully defined by its nodes and edges. In order to obtain both from chess positions obtained with functions presented in Chess Position Generation, ChessY provides several functions.
The function
getNodesFromPosition[ p ]returns a 1-dimensional list of length 64 with all node states in a given chess position p. An optional argument can be used to specify the type of state:
-
State->"Piece"state indicating individual type of chess pieces (see Table 2) -
State->"Color"(default)state indicating color of chess pieces (see Table 3) -
State->"Simple"state indicating whether node is occupied or not (see Table 4)
The returned list is of the form
{ NODE_1_STATE , NODE_2_STATE , ... }EXAMPLE:
The code
Get["ChessY.m"];
position = positionStart;
nodes = getNodesFromPosition[position,State->"Colors"];
Print[nodes];generates the output
The function
getEdgesFromPosition[ p ]returns a 2-dimensional list of all weighted edges in a given chess position p. Two optional arguments can be specified:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
-
SameColorTargetsTrue/Falseindicating whether edges are included for which both source and target nodes have same color. Please note that this argument must be set toFalsefor generating valid chess graphs!
default value:sameColorTargets->False
The returned list is of the form
{ { SOURCE , TARGET , WEIGHT } , { SOURCE , TARGET , WEIGHT } , ... }holding the set of all edges indicated by source node, target node and edge weight (state) information.
EXAMPLE:
The code
Get["ChessY.m"];
position = positionStart;
edges = getNodesFromPosition[position,State->"Simple"];
Print[edges];
generates the output
Finally,
getWhiteEdgesFromPosition[ p ]
getBlackEdgesFromPosition[ p ]are two internal functions used by getEdgesFromPosition[], and return 2-dimensional lists of all potential edges originating from white/black pieces (except edges from castling moves of the white/black king/rook) in a given chess position p.
Visualization
ChessY provides various functions for visualizing chess positions, positional chess graphs, and whole chess games. The function
showChessPosition[ p ]returns an array plot displaying a chess position p in the a classical (pieces on chessboard) style.
EXAMPLE:
The code
Get["ChessY.m"];
position = positionStart;
Print[showChessPosition[position]];
generates and visualizes the initial chess position:
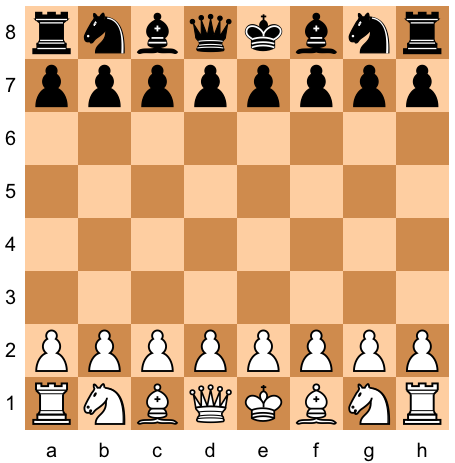
The function
showPositionalChessGraph[ NODES , EDGES ]returns chessgraph with given lists of NODES and EDGES, both generated with functions listed in Chess Graph Generation. For display reasons, nodes occupied by white/black pieces are colored in gray/black, unoccupied nodes as open circles. Edges originating from nodes occupied by white/black are colored in gray/black.
Various optional arguments are available:
-
ShowNodeIDTrue/False; displays the node ID in form of numbered nodes; note that this option only applies ifNodeLayout->"Chessboard"
default value:ShowNodeID->FalseGraphTypedefines which type of graph is generatedGraphType->"Color"(default)graph with"Color"edge/node statesGraphType->"Simple"simple graph with all nodes and edges displayed in one color ("Simple"edge/node states)
NodeLayoutdefines the node layout of the generated graphNodeLayout->"Chessboard"(default)nodes are arranged in a classical 8x8 chessboard layout, with arrows indicating directed edges between source and target nodesNodeLayout->"LinearV"nodes are arranged in a linear vertical fashion; edges originating from nodes occupied by white/black pieces are colored in gray/black; edges targeting nodes are drawn without arrows, as source is indicated by the edges' colorNodeLayout->"LinearH"nodes are arranged in a linear horizontal fashion; edges originating from nodes occupied by white/black pieces are colored in gray/black; edges targeting nodes are drawn without arrows, as source is indicated by the edges' color
EdgeLayoutspecifies the edge layout of the generated graphEdgeLayout->"Automatic"(default)Mathematica chooses the arrangement and style of edgesEdgeLayout->"Chessboard"the height of arched edges indicates the chessboard distance between source and target node
(this option only applies ifNodeLayout->"Linear")
ShowFrameTrue/Falsefor showing frame with tickmarks indicating the chessboard distance
default value:ShowFrame->FalseEXAMPLE:
The code
Get["ChessY.m"]; position = positionStart; nodes = getNodesFromPosition[position,State->"Color"]; edges = getEdgesFromPosition[position,State->"Color"]; g1 = showPositionalChessGraph[ nodes,edges, NodeLayout->"Chessboard",EdgeLayout->"Automatic",ShowFrame->False ]; g2 = showPositionalChessGraph[ nodes,edges, NodeLayout->"LinearV",EdgeLayout->"Chessboard",ShowFrame->True ]; Print[GraphicsGrid[{{g1,g2}}]];generates and visualizes two positional chess graphs (8x8 and linear vertical node layout) associated with the initial chess position:
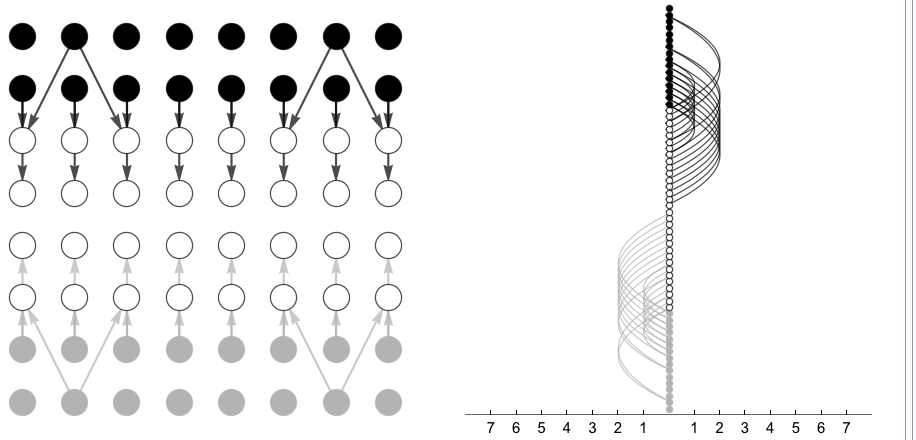
The function
animateChessPositions[ MOVES , POSITIONS ]returns a graphics displaying in an interactive fashion multiple chess positions, e.g. that of a chess game, given a list of moves and associated positions.
EXAMPLE:
The code
(* load the ChessY toolbox *) Get["ChessY.m"]; (* open PGN record file *) pgnfile = OpenRead["example2.pgn"]; eof = False; (* setup list for handling data *) game = Array[0,11]; { cEvent,cSite,cDate,cRound,cWhite,cBlack,cResult,cECO,cWhiteElo,cBlackElo,cMoves } = Table[i,{i,1,11}]; (* parse PGN record *) While[ !eof , If[ (record = Read[pgnfile,Record,RecordSeparators->{"\n"}])==EndOfFile , eof = True ]; If[ (!eof) && (StringTake[record,7]=="[Event ") , game[[cEvent]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,6]=="[Site ") , game[[cSite]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,6]=="[Date ") , game[[cDate]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[Round ") , game[[cRound]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[White ") , game[[cWhite]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[Black ") , game[[cBlack]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,8]=="[Result ") , game[[cResult]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,5]=="[ECO ") , game[[cECO]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,10]=="[WhiteElo ") , game[[cWhiteElo]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,10]=="[BlackElo ") , game[[cBlackElo]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,2]=="1.") , game[[cMoves]] = StringTrim[ StringSplit[record,RegularExpression["[0-9]+[\\.]"]] ] ]; ]; (* close PGN record file *) Close[pgnfile]; (* get list of moves and positions *) moves = game[[cMoves]]; positions = getPositionsFromGamePGN[moves]; (* animate chess game *) Print[animateChessPositions[moves,positions]];animates the game between Gundersen and Faul during the Pietzcker Christmas Tournament in 1928:
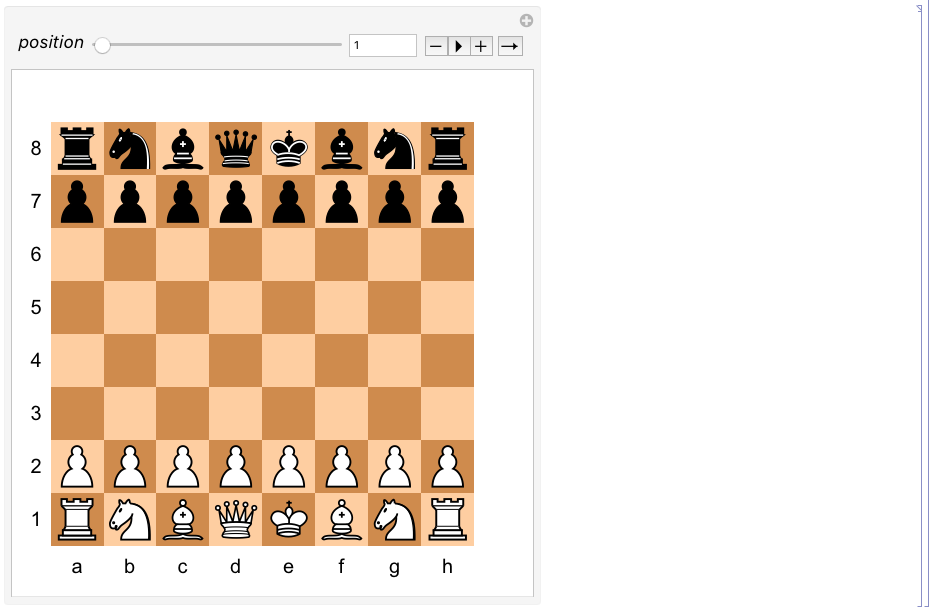
Finally, the function
animatePositionalChessGraphs[ NODES , EDGES ]returns a graphics displaying in an interactive fashion multiple positional chess graphs, given a list of nodes and edges associated with the positions of a chess game. The chess graphs displayed are the same to those generated by
showPositionalChessGraph[], thus the same optional arguments apply.EXAMPLE:
The code
(* load the ChessY toolbox *) Get["ChessY.m"]; (* open PGN record file *) pgnfile = OpenRead["example2.pgn"]; eof = False; (* setup list for handling data *) game = Array[0,11]; { cEvent,cSite,cDate,cRound,cWhite,cBlack,cResult,cECO,cWhiteElo,cBlackElo,cMoves } = Table[i,{i,1,11}]; (* parse PGN record *) While[ !eof , If[ (record = Read[pgnfile,Record,RecordSeparators->{"\n"}])==EndOfFile , eof = True ]; If[ (!eof) && (StringTake[record,7]=="[Event ") , game[[cEvent]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,6]=="[Site ") , game[[cSite]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,6]=="[Date ") , game[[cDate]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[Round ") , game[[cRound]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[White ") , game[[cWhite]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[Black ") , game[[cBlack]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,8]=="[Result ") , game[[cResult]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,5]=="[ECO ") , game[[cECO]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,10]=="[WhiteElo ") , game[[cWhiteElo]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,10]=="[BlackElo ") , game[[cBlackElo]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,2]=="1.") , game[[cMoves]] = StringTrim[ StringSplit[record,RegularExpression["[0-9]+[\\.]"]] ] ]; ]; (* close PGN record file *) Close[pgnfile]; (* get list of positions, nodes and edges *) positions = getPositionsFromGamePGN[game[[cMoves]]]; nodes = {}; edges = {}; For[ i=1,i<=Length[positions],i++, nodes = Append[nodes,getNodesFromPosition[positions[[i]]]]; edges = Append[edges,getEdgesFromPosition[positions[[i]]]]; ]; (* animate chess graph *) Print[ animatePositionalChessGraphs[ nodes,edges,ShowNodeID->False,GraphType->"Color",NodeLayout->"Chessboard" ] ];animates positional chess graphs associated with successive positions during the game between Gundersen and Faul during the Pietzcker Christmas Tournament in 1928:

Chess Graph Analysis
ChessY provides a baseline set of tools for analyzing positional chess graphs. However, with the knowledge of the data objects returned by ChessY, specifically position, node and edge lists, this set of tools can be easily extended utilizing the unlimited potential of Mathematica.
getNumberOfNodes[ NODES ]returns a list containing the number of nodes of a chess graph in specified states, taking a 1-dimensional list of nodes as argument. Options are:
-
Statespecifies the node states to be countedState->"Piece"- state indicating individual type of chess piecesState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
Depending on the chosen option, this function returns
- for
State->"Piece":{#wP,#wN,#wB,#wR,#wQ,#wK,#bK,#bQ,#bR,#bB,#bN,#bP} - for
State->"Color":{#white nodes,#black nodes} - for
State->"Simple":#occupied nodes
getNumberOfEdges[ EDGES ]returns the number of edges of a chess graph. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces on source node (default)State->"Simple"- state indicating whether source node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color":{#edges (white source nodes),#edges (black source nodes)} - for
State->"Simple":#edges
getAdjacencyMatrix[ EDGES ]returns the adjacency matrices $a_{ij}$ of a chess graph. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces on source node (default)State->"Simple"- state indicating whether source node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color": weighted adjacency matrix - for
State->"Simple": relational adjacency matrix
getConnectedness[ #EDGES ]returns the connectedness $\rho$ of a chess graph. If the argument is a list containing the number of edges originating from white and black nodes, the returned list contains the connectedness of the corresponding subgraphs, otherwise the total connectedness is returned.
getMobility[ NODES , EDGES ]returns the mobility $\mathcal{M}$ of a chess graph. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color": list with $\mathcal{M}$ of white and black nodes - for
State->"Simple": total $\mathcal{M}$
getControl[ NODES , EDGES ]returns the control $\mathcal{C}$ of a chess graph. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color": list with $\mathcal{C}$ of white and black nodes - for
State->"Simple": total $\mathcal{C}$
getDominance[ NODES , EDGES ]returns the dominance $\mathcal{D}$ of a chess graph. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color": list with $\mathcal{D}$ of white and black nodes - for
State->"Simple": total $\mathcal{D}$
getAverageNodeReach[ NODES , EDGES ]returns the dominance $\mathcal{R}$ of a chess graph. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color": list with $\mathcal{R}$ of white and black nodes - for
State->"Simple": total $\mathcal{R}$
getOffensiveness[ NODES , EDGES ]returns the offensiveness $O$ of a chess graph. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color": list with $O$ of white and black nodes - for
State->"Simple": total $O$
getDefensiveness[ NODES , POSITION ]returns the defensiveness $D$ associated with a chess position. Options are:
-
Statespecifies the edge state/weightState->"Color"- state indicating color of chess pieces (default)State->"Simple"- state indicating whether node is occupied or not
Depending on the chosen option, this function returns:
- for
State->"Color": list with $D$ of white and black nodes - for
State->"Simple": total $D$
EXAMPLE:
The code
(* load the ChessY toolbox *) Get["ChessY.m"]; (* generate position *) position = position23SpasskyFischer1972; (* get list of nodes and edges *) nodes = getNodesFromPosition[position,State->"Color"]; edges = getEdgesFromPosition[position,State->"Color"]; (* display positional chess graph *) Print[ showPositionalChessGraph[ nodes,edges,ShowNodeID->False,GraphType->"Color",NodeLayout->"Chessboard" ] ]; (* analyze chess graph *) aij = getAdjacencyMatrix[edges,State->"Color"]; nn = getNumberOfNodes[nodes,State->"Color"]; ne = getNumberOfEdges[edges,State->"Color"]; co = getConnectedness[ne]; m = getMobility[nodes,edges,State->"Color"]; c = getControl[nodes,edges,State->"Color"]; do = getDominance[nodes,edges,State->"Simple"]; r = getAverageNodeReach[nodes,edges,State->"Color"]; o = getOffensiveness[nodes,edges,State->"Color"]; d = getDefensiveness[nodes,position,State->"Simple"]; (* print results *) Print["number of nodes = ",nn]; Print["number of edges = ",ne]; Print["connectedness = ",co]; Print["mobility = ",m]; Print["control = ",c]; Print["dominance = ",do]; Print["average node reach = ",r]; Print["offensiveness = ",o]; Print["defensiveness = ",d];generates the output:
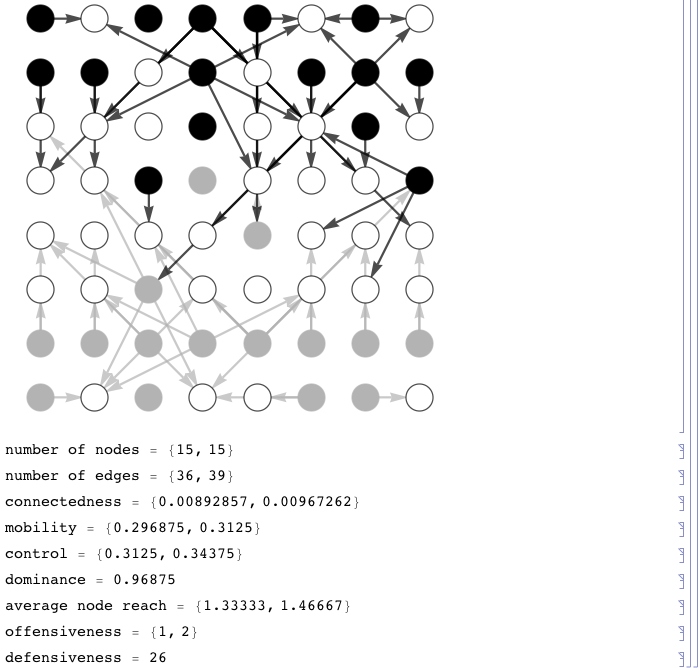
Examples
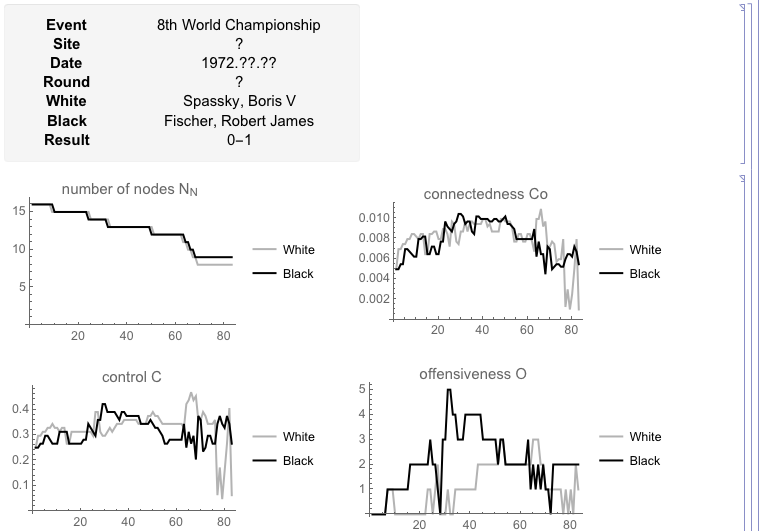
Analysis of a Chess Game
Input:
(* load the ChessY toolbox *) Get["ChessY.m"]; (* open PGN record file *) pgnfile = OpenRead["example3.pgn"]; eof = False; (* setup list for handling data *) game = Array[0,11]; { cEvent,cSite,cDate,cRound,cWhite,cBlack,cResult,cECO,cWhiteElo,cBlackElo,cMoves } = Table[i,{i,1,11}]; (* parse PGN record *) While[ !eof , If[ (record = Read[pgnfile,Record,RecordSeparators->{"\n"}])==EndOfFile , eof = True ]; If[ (!eof) && (StringTake[record,7]=="[Event ") , game[[cEvent]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,6]=="[Site ") , game[[cSite]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,6]=="[Date ") , game[[cDate]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[Round ") , game[[cRound]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[White ") , game[[cWhite]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,7]=="[Black ") , game[[cBlack]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,8]=="[Result ") , game[[cResult]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,5]=="[ECO ") , game[[cECO]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,10]=="[WhiteElo ") , game[[cWhiteElo]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,10]=="[BlackElo ") , game[[cBlackElo]] = StringSplit[record,"\""][[2]] ]; If[ (!eof) && (StringTake[record,2]=="1.") , game[[cMoves]] = StringTrim[ StringSplit[record,RegularExpression["[0-9]+[\\.]"]] ] ]; ]; (* close PGN record file *) Close[pgnfile]; (* get list of game positions from moves *) positions = getPositionsFromGamePGN[game[[cMoves]]]; (* print result *) Print[ Panel[ Text[ Grid[ { { Style["Event \t",Black,Bold,FontFamily->"Arial",FontSize->12 ], Style[game[[cEvent]],Black,FontFamily->"Arial",FontSize->12 ] }, { Style["Site \t",Black,Bold,FontFamily->"Arial",FontSize->12 ], Style[game[[cSite]],Black,FontFamily->"Arial",FontSize->12 ] }, { Style["Date \t",Black,Bold,FontFamily->"Arial",FontSize->12 ], Style[game[[cDate]],Black,FontFamily->"Arial",FontSize->12 ] }, { Style["Round \t",Black,Bold,FontFamily->"Arial",FontSize->12 ], Style[game[[cRound]],Black,FontFamily->"Arial",FontSize->12 ] }, { Style["White \t",Black,Bold,FontFamily->"Arial",FontSize->12 ], Style[game[[cWhite]],Black,FontFamily->"Arial",FontSize->12 ] }, { Style["Black \t",Black,Bold,FontFamily->"Arial",FontSize->12 ], Style[game[[cBlack]],Black,FontFamily->"Arial",FontSize->12 ] }, { Style["Result \t",Black,Bold,FontFamily->"Arial",FontSize->12 ], Style[game[[cResult]],Black,FontFamily->"Arial",FontSize->12 ] } } ] ] , FrameMargins->{{30, 30}, {10, 10}} ] ]; (* get list of moves, positions, nodes and edges *) moves = game[[cMoves]]; positions = getPositionsFromGamePGN[ moves ]; nodes = {}; edges = {}; For[ i=1,i<=Length[positions],i++, nodes = Append[nodes,getNodesFromPosition[positions[[i]]]]; edges = Append[edges,getEdgesFromPosition[positions[[i]]]]; ]; (* analyse all positions of game *) nn = {}; ne = {}; co = {}; m = {}; c = {}; do = {}; r = {}; o = {}; d = {}; For[ i=1,i<=Length[positions],i++, nn = Append[nn,getNumberOfNodes[nodes[[i]],State->"Color"]]; ne = Append[ne,getNumberOfEdges[edges[[i]],State->"Color"]]; co = Append[co,getConnectedness[ne[[i]]]]; m = Append[m,getMobility[nodes[[i]],edges[[i]],State->"Color"]]; c = Append[c,getControl[nodes[[i]],edges[[i]],State->"Color"]]; do = Append[do,getDominance[nodes[[i]],edges[[i]],State->"Color"]]; r = Append[r,getAverageNodeReach[nodes[[i]],edges[[i]],State->"Color"]]; o = Append[o,getOffensiveness[nodes[[i]],edges[[i]],State->"Color"]]; d = Append[d,getDefensiveness[nodes[[i]],positions[[i]],State->"Color"]]; ]; (* display some of the results *) g1 = ListPlot[ Transpose[MapIndexed[{{First@#2,#1[[1]]},{First@#2,#1[[2]]}} &, nn]], PlotRange->All, Joined->True, PlotLabel->"number of nodes, PlotLegends->{"White","Black"}, PlotStyle->{GrayLevel[0.7],Black} ]; g2 = ListPlot[ Transpose[MapIndexed[{{First@#2,#1[[1]]},{First@#2,#1[[2]]}} &, co]], PlotRange->All, Joined->True, PlotLabel->"connectedness", PlotLegends->{"White","Black"}, PlotStyle->{GrayLevel[0.7],Black} ]; g3 = ListPlot[ Transpose[MapIndexed[{{First@#2,#1[[1]]},{First@#2,#1[[2]]}} &, c]], PlotRange->All, Joined->True, PlotLabel->"control", PlotLegends->{"White","Black"}, PlotStyle->{GrayLevel[0.7],Black} ]; g4 = ListPlot[ Transpose[MapIndexed[{{First@#2,#1[[1]]},{First@#2,#1[[2]]}} &, o]], PlotRange->All, Joined->True, PlotLabel->"offensiveness", PlotLegends->{"White","Black"}, PlotStyle->{GrayLevel[0.7],Black} ]; Print[GraphicsGrid[{{g1,g2},{g3,g4}}]];Output: